Что делать если площадь отрицательная

Форумы GIS-Lab.info
Делалось так в ручном режиме: все неотзеркаленые части впихивались в пространство от 0 до 1. Значение может быть отрицательное. Если залить в бутылку 1л воды и повернуть её на 30 градусов вдоль любой оси, там по прежнему будет 1л воды. И никогда там не станет -1л воды. Этому препятствуют две вещи, во первых потеря точности при флиппинге, во вторых тот самый факт, ради которого я тему создал.




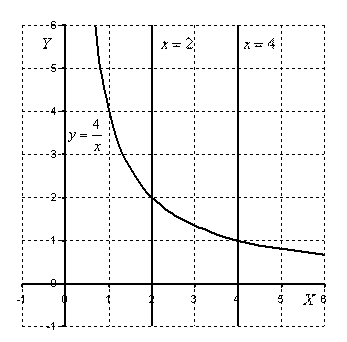
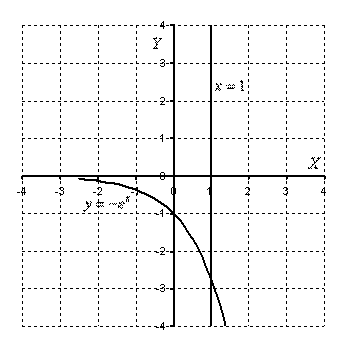


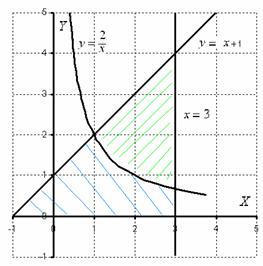

В формуле векторным произведением координат и сложением определяется площадь области, охватывающей многоугольник, а затем из нее вычитается площадь окружающего многоугольника, что дает площадь многоугольника внутри. Также она называется формулой шнурования, так как положительные и отрицательные слагаемые, состоящие из перемножаемых координат, располагаются крест-накрест, как при завязывании шнурков. Она находит применение в геодезии , лесном хозяйстве и других областях. Формула была описана Мейстером — в году и Гауссом в году. Она может быть проверена путём деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина.





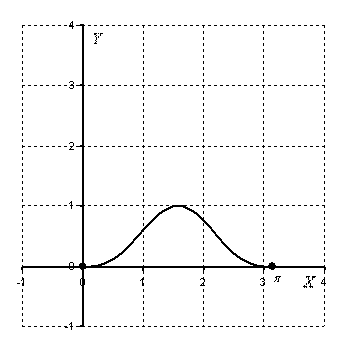


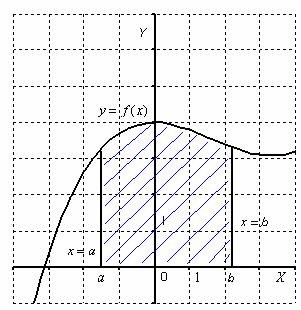


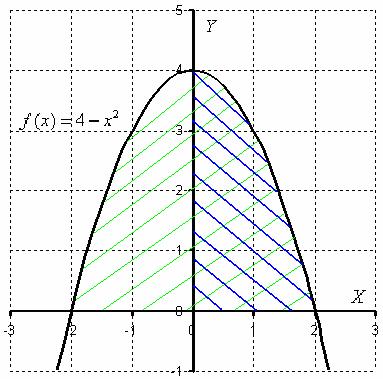
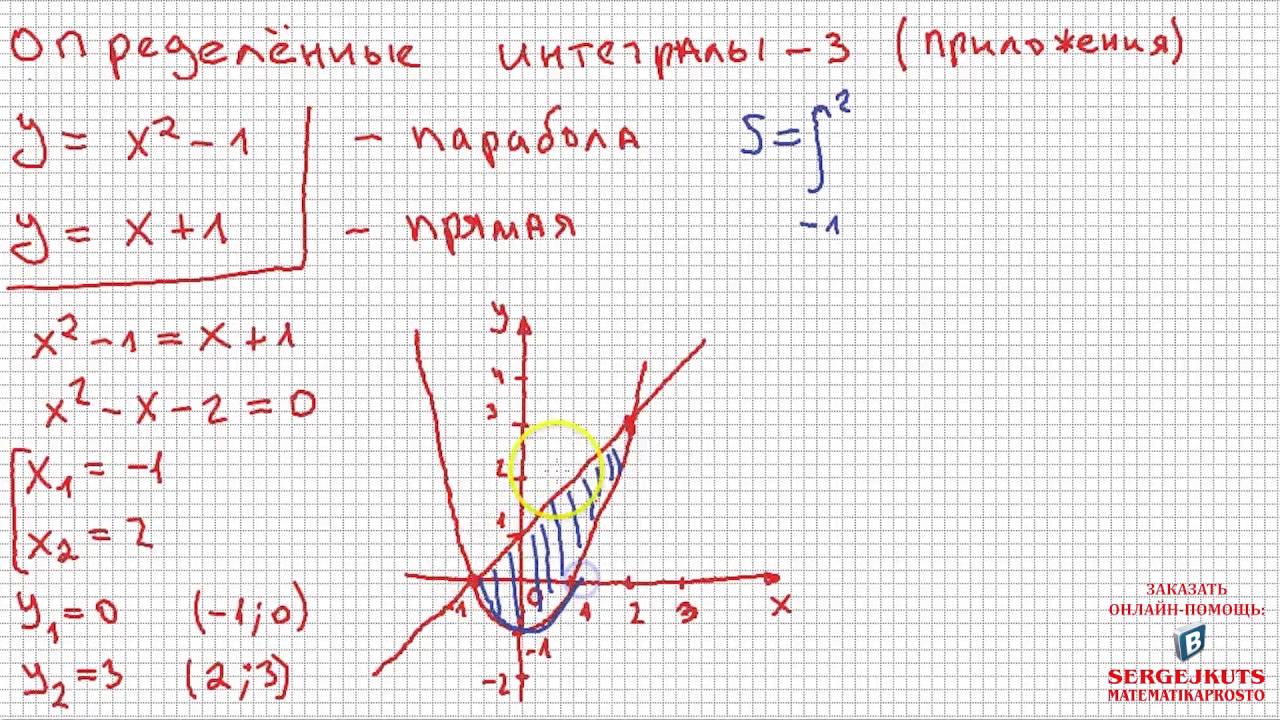
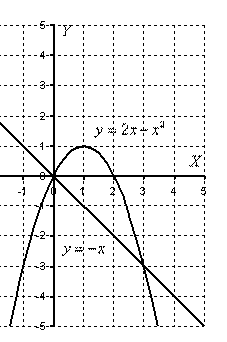
Сегодня мы рассмотрим, как с помощью определённого интеграла найти площади разных фигур на плоскости в декартовой системе координат. Это свойство определённого интеграла используется очень часто при решении многих подобных задач. И я расскажу об основных видах таких задач в этой статье. Теперь перейдём к возможным вариантам расположения фигур, площадь которых надо вычислить на координатной плоскости.